
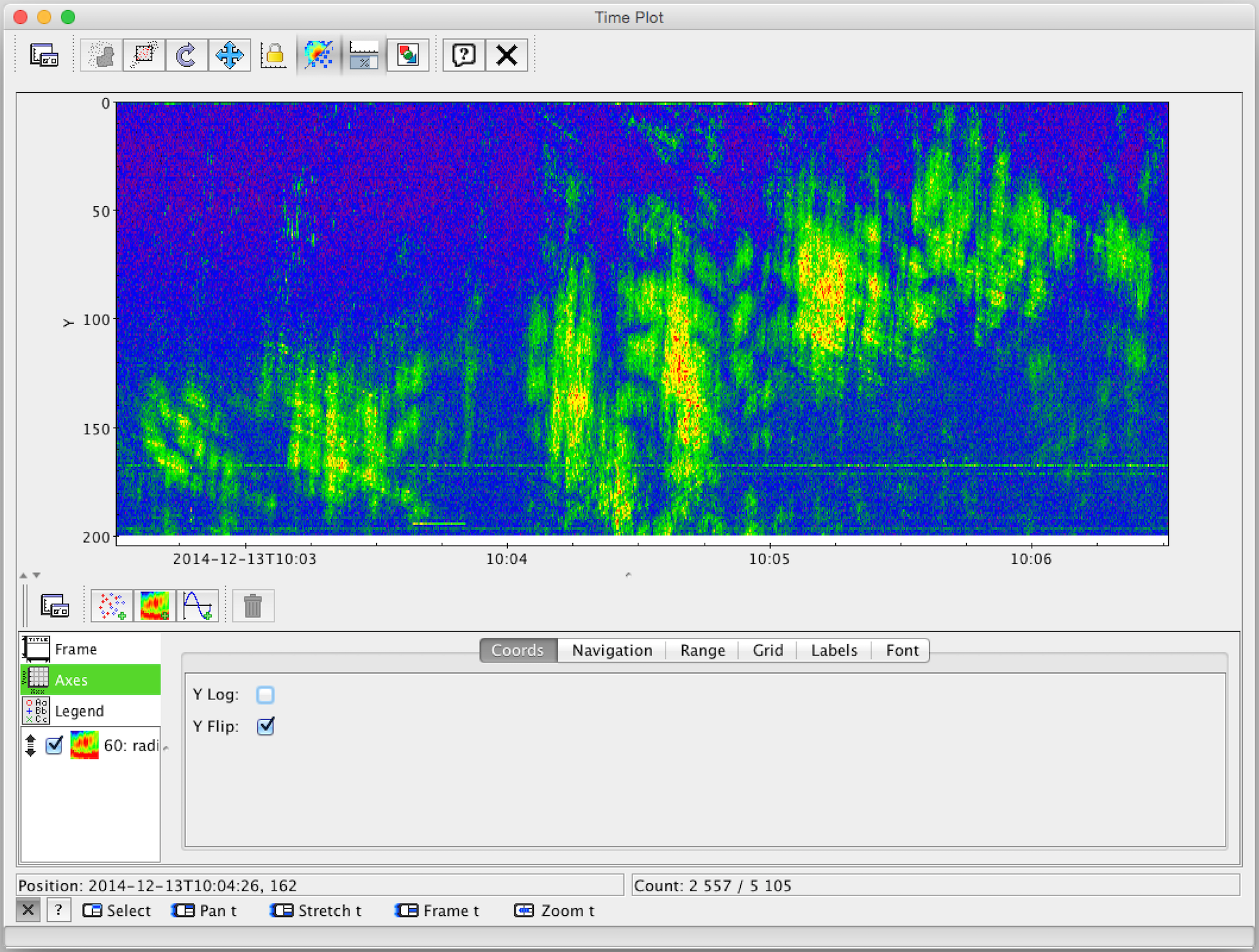
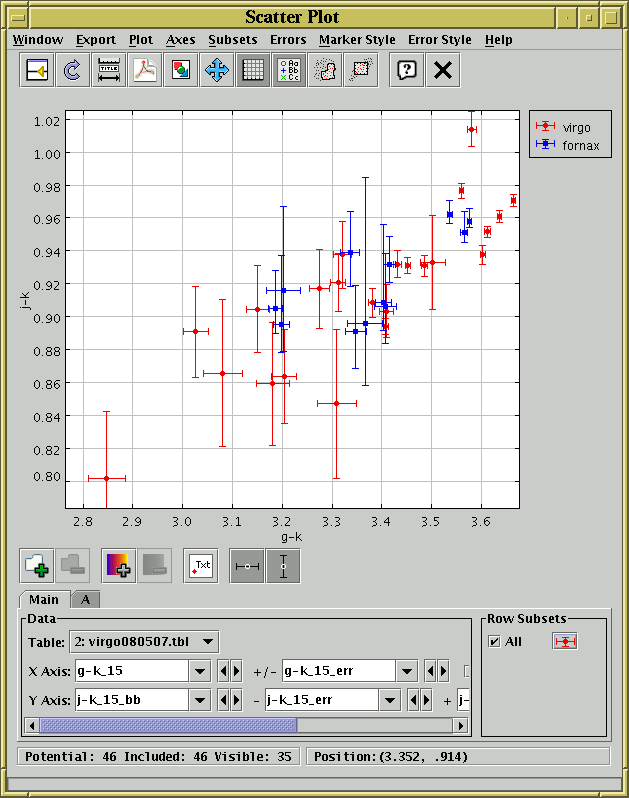
#Topcat astronomy full
The dynamical system used is the Restricted Full Three Body Problem, with the primaries, an elongated body and a sphere, in a short axis relative equilibrium configuration. In this paper we have analysed and compared two different schemes to compute Poincaré maps in the context of accuracy versus computation time: a Runge-Kutta method of 7th and 8th order and a time transformed geometric method of 6th order. Poincaré maps are however time consuming to compute. Poincaré maps are a basic dynamical systems tool yielding information about the geometric structure of the phase space of the system. This additional Doppler broadening of the line profile function removes the central dip typical to the Holtsmark profile. The multi-component Stark splitting of the hydrogenic spectral lines and the modeled stochastic electron transitions in the electric field of the adjacent ions generate wide Doppler plateaux at the line centers, with the characteristic widths estimated from the fit to the characteristic width of the Holtsmark profile. In the intermediate part of the line, the parabolic cylinder functions expressed via the confluent hypergeometric series, are used.
#Topcat astronomy series
We get well converging series expansions for the line wings and centers by reducing the number of arguments in the profile function by one, introducing the module of the Holtsmark and Lorentz profiles as a new argument. Analytical series expansions for the hydrogenic spectral line profile functions are derived starting from the three single expressions, obtained by integrating twice the convolution of the Holtsmark, Lorentz and Doppler line profile functions.


 0 kommentar(er)
0 kommentar(er)
